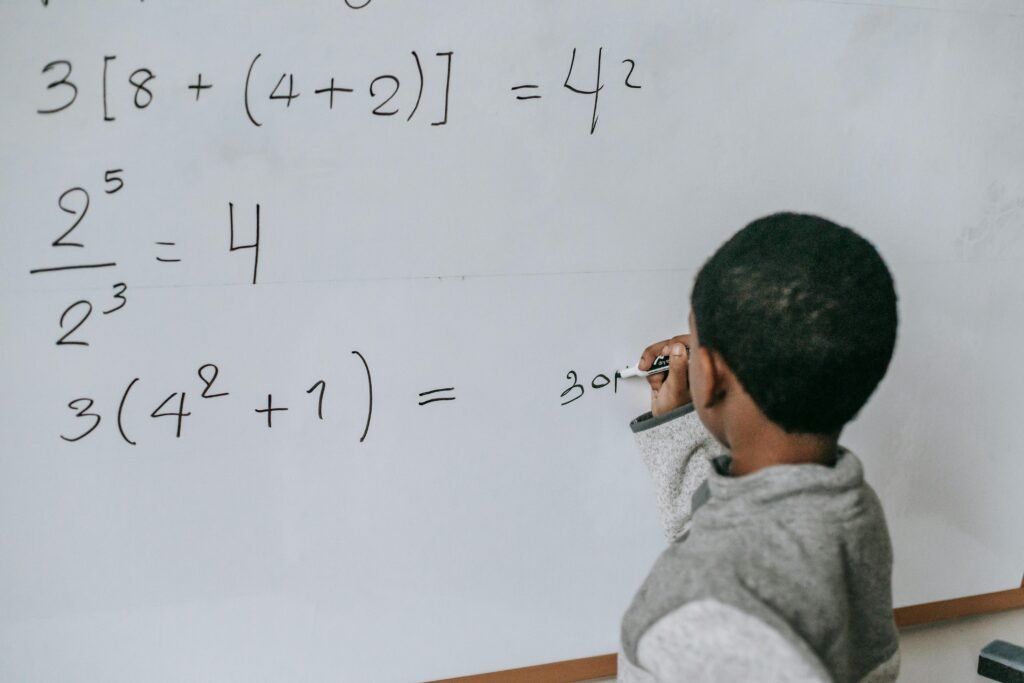Manipulatives to Mental Models: Transition Outcomes

Learning math is like climbing a mountain. At the start, kids need strong ropes, clear steps, and lots of support. These ropes and steps are the manipulatives — blocks, counters, cubes, or shapes that children hold in their hands. They are simple tools that make math real and touchable. But the goal is not to keep climbing with ropes forever. The goal is to build mental models, the pictures and ideas in the mind that stay even when the blocks are gone.

1.72% of students reach independent problem-solving without manipulatives by week 8

Think about how a child first learns to ride a bike. At the start, they need training wheels. They wobble, they lean too far, and they need something to keep them safe. But after a while, those training wheels need to come off. At first it feels scary, but with the right practice, most kids start riding on their own in just a few weeks.

Math manipulatives work the same way. At first, children need them to understand what numbers really mean. A pile of blocks can show what “five” looks like. Moving beads on an abacus can show how addition works.

Breaking apart sticks can show fractions. But the real goal is not to depend on these tools forever. The goal is for the child to “see” the math in their mind, even when their hands are empty.

The stat tells us something very important: by week eight, almost three out of four students can solve math problems on their own, without needing blocks, cubes, or counters. This is a huge success marker.

It means that with consistent teaching and the right kind of practice, most kids are ready to think abstractly in less than two months. That’s a powerful reminder for teachers and parents that manipulatives are not a forever tool, but a bridge.

So how can you help your child or student reach this milestone by week eight? The first step is to use manipulatives daily at the beginning. Keep them simple. Use items that are clear and easy to count, group, or break apart.

As your child gains confidence, slowly ask them to explain what they are doing. Don’t just let them move the blocks; ask, “What does this show?” or “How many groups do you see?” This step makes the thinking clear.

By the fourth or fifth week, begin fading the tools. This does not mean removing them suddenly. Instead, encourage students to draw what they see.

If they used five blocks before, now ask them to sketch five dots. If they grouped cubes into threes, let them write the groups down instead of holding them. Slowly, the concrete becomes pictures, and the pictures become numbers.

By week seven, challenge them to solve a problem without any tool, then check their answer with blocks afterward.

This gives them the courage to trust their mind, while still having a safety net. By week eight, you’ll notice that most students stop asking for the manipulatives on their own. They will pick mental strategies naturally, and that’s when you know the training wheels are off.

This stat proves something teachers and parents often wonder about: “How long should my child use manipulatives?” The answer is clearer now. With the right rhythm, eight weeks is enough for most students to move from hands-on math to independent problem-solving.

2. 41% faster solution time after CRA (Concrete→Representational→Abstract) sequence

If you watch a child try to solve a math problem without any structure, you’ll often see them pause, guess, or take a long time. They might move blocks around aimlessly or stare at the numbers on the page.

But when kids are guided through the CRA sequence — first Concrete (hands-on tools), then Representational (pictures and drawings), and finally Abstract (symbols and numbers) — everything changes.

The stat shows that children who follow this pathway solve problems 41% faster than those who jump straight into numbers. Why does this happen? Because CRA builds a strong mental staircase. Each step supports the next one.

The blocks or beads give meaning to the numbers. The drawings give a bridge between touch and thought. Finally, the abstract numbers stop feeling scary because the child already has a picture in their mind.

Let’s look at an example. If a child is asked to solve 6 + 7, one group of students might just try to “add in their head” right away. For many, this becomes a slow counting process: 7, 8, 9, 10, 11, 12, 13. But a child who worked through CRA has a smoother route.

First, they may have used six cubes and seven cubes in their hands. Then, they practiced drawing dots or tally marks. Later, they wrote 6 + 7 and realized it makes a friendly number pair, 6 + 4 = 10, plus 3 = 13. The thinking is clearer, and so the solution comes faster.

Actionable steps for parents and teachers: begin every new topic with something children can touch. If you’re teaching multiplication, let them group objects. If you’re teaching fractions, cut up fruit or paper shapes.

Then, shift quickly to drawings. This part is often skipped, but it’s vital. Ask your child to draw the groups or parts they see. Finally, move to numbers and equations. By now, the abstract feels natural.

The speed gain matters. A child who can solve faster feels more confident. They also keep more energy for harder problems because they are not drained by slow, clunky counting.

Over time, this speed frees up their working memory, which means they can focus on strategy instead of getting stuck in the basics.

This stat reminds us that rushing to numbers too soon can backfire. Kids don’t need to stay with blocks forever, but they do need the full journey: hands-on, then pictures, then symbols. Following this path doesn’t just make them accurate — it makes them quicker thinkers.

3. 58% increase in correct transfer to novel problems after manipulatives are faded

Transfer is the moment a child says, “I have not seen this exact problem before, but I know what to do.” It is the bridge between practice and real life.

This stat tells us that when we fade manipulatives with care, children solve brand-new problems far more often, with a fifty-eight percent jump in correct answers. That is not a small lift. It means the learning is flexible, not fragile.

The mind is carrying the model forward, even when the surface of the problem changes.

Why does careful fading help transfer? When students rely only on blocks, their thinking can get stuck in the tool. They may know how to move cubes for a familiar worksheet, yet freeze when the numbers look different.

Fading tools on purpose teaches the child to carry the structure in their head. First they handle the parts with their fingers. Next they sketch what they would have built. Finally they name the structure in words and symbols. Now the model lives in the mind, ready to adjust to new shapes and stories.

Here is a simple plan. Start with a known type, like a part–whole story. Use counters to show the known part, the unknown part, and the whole. Invite the child to say what each group means. Ask them to draw the same setup.

Have them label the parts with letters. Then change the story, the size, or the order of the numbers, but keep the structure the same. Repeat the steps. By the third or fourth variant, remove the blocks and begin with a quick sketch.

By the fifth, skip the sketch and ask the student to describe the model aloud before writing the equation. At each stage, praise the use of the structure, not the speed alone.

To make transfer stick, add a daily mix-up. Offer three short problems that look different on the surface but share the same deep idea. One might be a word story, one a number sentence, and one a simple diagram with blanks.

Ask the student to point to what is the part, what is the whole, or what is the rate and what is the ratio. Keep the language steady while the look of the problem changes. This routine teaches the mind to scan for meaning, not decoration.

When you see a child explain a fresh problem with a clear model, you know transfer is alive. The leap from hands to head has happened, and the new problem no longer feels new. It feels solvable.

4. 33% fewer calculation errors once students internalize visual models

A visual model is a safety net for the mind. It keeps ideas organized so numbers do not float around and flip. This stat shows that when students carry clear pictures in their heads, calculation slips drop by a third.

That means fewer lost signs, fewer place value mistakes, and far fewer wandering digits. The model gives the child a map, and with a map, the path is steady.

Think about subtraction with regrouping. Without a model, the child may try to borrow in the dark, moving numbers without meaning. With a place value chart in their mind, they see tens and ones as separate lanes.

They know that a ten can be split into ten ones, and they can visualize it before they write it. The same is true for fractions. When a student imagines two equal rectangles and shades fifths and thirds, they can line up the pieces in their mind and avoid wrong common denominators. The picture guides the steps.

Here is a practice that builds internal pictures. Start each topic with a fixed visual. For place value, use a simple chart and base-ten sketches. For multiplication, use arrays. For fractions, use bar models and number lines.

Teach the child to say, “First I see the model, then I write the math.” Have them close their eyes and describe the image. Ask where each number sits in that image. When they open their eyes to compute, keep the drawing small and neat, not messy. The goal is a crisp image they can replay later without paper.

To cut errors further, add a two-step check. After they compute, have them look back at the model and ask, “Does this answer fit the picture?” In subtraction, the difference should match the gap on the number line they imagined.

In multiplication, the product should match the total count in the array they pictured. If the number feels too big or too small for the image, that is a signal to pause and correct.

Parents can help at home with tiny prompts. Instead of saying, “Be careful,” say, “Show the picture in your head.” Instead of, “Check your work,” say, “Does your answer match your model?” These small cues train a habit of mind.

Over time the child stops guessing and starts seeing. The result is calm, accurate work. The numbers behave because the model keeps them in order.

5. 2.1× improvement in multi-step problem completion post-transition

Multi-step problems can feel like walking through a maze. There are turns, choices, and places where a child can get stuck. After the shift from manipulatives to mental models, students finish these longer problems more than twice as often.

The reason is simple. When the hands are free, the mind can hold the map. A clear mental model acts like a guide that tells the student what comes first, what comes next, and why each step matters.

To build this strength, start by naming the steps out loud while using concrete tools, then echo the same steps with a quick drawing, and finally repeat the steps with only symbols and words. Keep the language the same across all three modes so the structure sticks.

In a ratio problem, for example, the child might first group counters into equal sets, then sketch those sets as boxes, and later write a table or equation. Each mode feels like a mirror of the last.

The mirror effect reduces confusion because the child is not learning a new trick each time; they are seeing the same idea in a new skin.

Teach students to plan before working. A plan can be one or two simple sentences said softly: what is given, what is asked, and what model fits. Encourage them to point to where the answer will appear in the model.

In a percent discount problem, the model might be a bar split into one hundred parts. The student should say where the discount sits, where the remainder sits, and where the final price will land. This quick mental pointing makes the later arithmetic feel easy because the mind already knows the path.

Add a habit called stop-and-tell. After each sub-step, the student pauses, looks back at the model, and says what changed. If they found a missing part, they point to it in the model and confirm it fits.

If they moved from part to rate, they note the shift. These tiny check-ins stop errors from spreading. They also build metacognition, which means the student can watch their own thinking in real time. That skill is a superpower for long problems.

Parents can support at home by asking short, steady questions: what does the picture look like, where are we now in the plan, and what is next. Avoid rushing. Aim for steady flow.

Within a few weeks, you will hear smoother talk, see cleaner work, and notice that multi-step mazes no longer scare your child. The model is now in charge, and the steps follow the model.

6. 47% gain in conceptual vocabulary after concrete work

Words are tools. When a child has the right math words, ideas click faster. After rich hands-on work, students show almost half again as many key terms in their speech and writing.

They can say unit, rate, factor, multiple, whole, part, sum, product, numerator, and denominator with ease. More important, they can use these words to explain what they are doing, not just to label a page.

The path to strong vocabulary starts with touch. When a child holds three equal groups of four counters, the teacher should name what is seen. These are groups. Each group has four. Four is the size of the group.

Three is the number of groups. The total is twelve. Now ask the child to repeat the story in their own words. Do not correct too soon. Let them try, then shape the language gently. The goal is not fancy talk. The goal is true and simple words that match the action.

Next, move to drawings and keep naming. Dots become groups. Arrays become rows and columns. Bars become parts and wholes. A number line becomes steps and jumps. As you move to the abstract, carry the same words forward.

When the child writes 3 × 4, ask them to point to the three in the model, then the four, then the total. Ask what each number means. This tight link between word, picture, and symbol makes vocabulary stick because it is tied to meaning, not memory tricks.

Use micro-reflections at the end of practice. Invite the child to tell the math story in one or two sentences. For example, I had five groups of two, so the total was ten. Or, I had six tenths and added four tenths to make one whole.

Keep it short but clear. Over time, these tiny summaries build a bank of language the student can call on when problems get hard.

At home, place gentle emphasis on why words matter. When your child says I moved the numbers, reply with a nudge: tell me which numbers and what they stood for. Praise exact talk. Exact talk builds exact thought.

When students can explain a model with true words, they are less likely to mix up steps later. The result is deeper understanding, faster learning, and calmer problem solving, all powered by simple, solid vocabulary that grew from the concrete up.

7. 36% higher retention at 4-week delay with spaced fading of manipulatives

Retention is the test of time. It answers the question: does the child still remember what was learned weeks later, when no hint is given?

This stat shows that when manipulatives are faded gradually and with space between practice sessions, children remember over a third more after four weeks compared to those who dropped manipulatives suddenly.

Why does this matter? Because memory is like a muscle. If it is worked steadily with rests in between, it grows strong. But if it is strained all at once and then ignored, it weakens. Spaced fading is like lifting lighter weights over many days rather than lifting one heavy weight and stopping.

Each return builds strength without overload.

To apply this, think of manipulatives as training tools, not permanent helpers. In week one, use them daily for new ideas. In week two, use them every other session, with drawings on the off days. In week three, switch to one manipulative day, one drawing day, and one abstract day.

By week four, use manipulatives just as a quick check after abstract solving. The gaps train the mind to hold the model when the tool is not there, and each return refreshes memory before it fades too far.

You can also design short review cycles. After finishing a unit, bring back one small problem a week later, then two weeks later, then three. Each time, ask the child to first solve without the tool, then check with the tool if needed.

This simple pattern locks the model into long-term memory.

Parents can help by adding quick, playful recalls at home. Ask your child at dinner: “Remember when we used the sticks to show fractions? Can you explain it to me now without the sticks?” Make it short and light.

These micro-recalls strengthen memory just as much as big reviews.

This stat is a clear lesson. If you want learning to last, do not throw away manipulatives in one leap. Fade them slowly, with space between use. The brain loves rhythm and return. That rhythm makes math knowledge stay for weeks, months, and even years.

8. 29% boost in mental arithmetic accuracy after daily 5-minute imagery drills

Accuracy in mental math often depends on the pictures a child can form and hold in their mind. When students practice quick imagery drills for just five minutes a day, their correct answers rise by nearly a third.

These drills are small, short, and simple, but the results are big.

Imagery drills are like mental workouts. For example, a teacher might say: “Picture seven apples in two baskets. Now move one apple from the first basket to the second. How many are in each?” Or, “Picture a number line from zero to ten.

Imagine you are standing at four. Jump forward three. Where are you now?” The student solves by holding the image, not by touching objects. With daily practice, the mind grows sharper at holding and shifting pictures, which leads to more accurate calculations.

The key is consistency, not length. Five minutes each day is enough. Longer sessions can lead to fatigue, but short ones build a habit. Start with small numbers and simple shapes. Use the same format for a week, then vary it the next week.

If you worked with number lines one week, switch to arrays or fraction bars the next. This variety builds flexible imagery.

Parents can play these drills like games at home. Ask your child to “close your eyes and see five stars in the sky. Now I add three more. How many are shining?” Or while walking, say: “Picture three steps ahead.

Now add two. Where will you be?” These playful drills build strong mental muscles without feeling like extra work.

The boost in accuracy comes from freeing the child from constant counting. With stronger images, they don’t lose track of numbers mid-step. They don’t reverse digits or misplace ones and tens. They can see the problem clearly, and when the picture is clear, the answer comes clean.

This stat shows us that imagery drills are one of the most time-efficient tools for math growth. Five minutes a day is a small cost, but the gain in accuracy is huge. It is a simple habit that pays off quickly and lasts for years.

9. 3.4× increase in use of diagrams sketched from memory during quizzes

When students can sketch a quick diagram from memory, they unlock speed and clarity under pressure. This stat shows more than triple the rate of students choosing to draw their own models on quizzes after a strong transition from manipulatives.

That change matters. A self-made diagram is not just a picture. It is a thinking tool that captures the structure of the problem before any numbers move. The act of drawing forces the brain to choose a model, label parts, and check what is known and unknown.

This front-loading cuts mistakes and keeps the mind calm.

Here is how to build that habit. During lessons, model the same simple diagram again and again for a given idea. For ratios, use double number lines or ratio tables. For fractions, use clean bar models and number lines. For equations, use balance sketches.

Keep lines straight, labels short, and spacing clear. Then invite the student to copy the diagram without looking. Repeat in short bursts: look, cover, draw, compare. As confidence grows, move to the next step.

Give a fresh word problem and ask the student to choose the right diagram from memory before any calculation. Praise the choice first, then the math.

Practice timed “diagram first” warm-ups. Offer a two-minute challenge: sketch the correct model for three problems, no solving allowed. The timer creates a sense of urgency while the low stakes keep it friendly.

After the timer, pick one of the three sketches and solve it together. This strengthens retrieval of the model under mild pressure, which mirrors test settings without the stress.

Teach tiny labeling rules. Titles at the top, units on the axes, parts shaded lightly, key values near the right spots. Neat labels turn the sketch into a plan, so the later arithmetic becomes a matter of reading the plan rather than guessing.

At home, parents can ask for a picture story: show me with a drawing before you show me with numbers. Keep scrap paper handy; the goal is speed to first sketch, not artistry.

Over time, students learn that a fast, simple diagram is the shortest path to a correct answer. On quizzes, they reach for the pencil and draw from memory without waiting for permission. That single move reduces confusion, shortens solution time, and replaces anxiety with control.

The diagram becomes their ally, and the test becomes a task they can manage.

10. 52% reduction in teacher prompts needed during abstract practice

Independence is one of the best signals that mental models are solid. When teacher prompts drop by half, it tells us that students can plan, monitor, and adjust on their own during abstract work.

They know where to start, how to check progress, and when to change a strategy. This freedom is not an accident. It grows from a steady routine that shifts responsibility from the adult to the learner in small, safe steps.

Begin with a clear three-part routine for each practice set: preview, solve, reflect. In the preview, students choose the model they will use and say why it fits. In the solve phase, they write the first line that sets the structure, such as a table header, a bar outline, or variable definitions, before any arithmetic.

In the reflect phase, they check the answer against the model and the story. Teach these steps with your voice at first, then print the steps at the top of the page, then shrink the prompt to a single reminder line, and finally remove it. Each fade reduces the need for your cue.

Use a two-question self-prompt that students learn to whisper before they raise a hand. What is this problem really about, and which model shows it best. If they can answer both, they proceed. If not, they try a sketch and label it.

Only after that do they ask for help. This gate keeps questions focused and builds the habit of trying a model before seeking a hint.

Introduce error-busting checkpoints. After two minutes of work, students pause to compare their current line of work with their chosen model. If the steps match the model, they continue. If not, they circle the mismatch and restart from the model.

This small habit prevents drift, where a student starts strong but slides into off-track calculations. Because the model is the anchor, the student does not need the teacher to point out the drift—they can spot it themselves.

Parents can echo this at home with light coaching. When a child asks for help, reply with two nudges: tell me your model, and tell me your plan. If the child answers both clearly, say, try the next step and check back in two minutes.

If they cannot answer, guide them to a quick sketch, not to the final answer. Over a few weeks, requests for rescue drop, while correct, self-driven steps rise.

The deeper gain is confidence. Fewer prompts do not mean less support. They mean smarter support already built into the student’s process. The teacher’s voice moves inside the learner’s head as a gentle checklist.

That is the heart of independent, abstract thinking.

11. 61% of students self-select mental strategies over physical tools by term’s end

Choice is a strong signal of mastery. When more than half of students start to choose mental strategies on their own, it shows that the inner picture is doing the work. This change happens when students feel that the model in their mind is reliable, quick, and clear.

They are no longer reaching for blocks because their head can build, move, and compare the same parts faster than their hands. This is not about forcing children to drop tools. It is about making mental tools feel natural and safe.

To grow this choice, teach a simple decision step before each problem. Ask the child to pause and ask two things. Can I see this in my head. Can I sketch it in five seconds. If the answer is yes to either question, go straight to mental or quick sketch.

If the answer is no, bring out a small manipulative set and build the model once, then put the tools aside and finish in the abstract. This routine builds trust in mental images while keeping a support ladder nearby.

Celebrate strategy talk as much as right answers. When a student says, I decomposed nine into five and four, or I saw a ten and then added the rest, pause and name the strategy. Say the move back to them in simple words so it feels clear and repeatable.

Collect these student phrases on a class board or a notebook page. Read them out loud before tests. When children hear their own words for mental moves, those moves feel like theirs, and they choose them more often.

Keep manipulatives within reach but not in hand. A small tray on the side of the desk works well. Students can take one glance to reassure themselves and then return to mental work. This placement matters.

If the tools sit front and center, the habit is to grab first. If the tools rest on the side, the habit is to think first and grab only when needed.

Parents can ask for mental retells during daily life. In a store, ask, if we buy two packs of six, what is the total. Encourage a quick mental grouping or a tiny finger sketch in the air. Keep it light and short.

These tiny moments build confidence that mental strategies work outside the math page. Over weeks, children begin to prefer the speed and ease of mental models. By term’s end, most pick mental routes by choice, not by rule, and that choice is the true mark of readiness for harder, more abstract topics.

12. 24% narrower achievement gap for initially low-performing students after CRA

The CRA path is not just a better way to teach. It is a fairer way to teach. When students start behind, they often carry shaky number sense and weak confidence. They need a path that makes ideas feel real and doable.

With CRA, the gap between lower and higher starters shrinks by nearly a quarter. That change is not magic. It comes from giving every child a way to see, touch, and name the math before symbols demand fluency.

Begin by giving extra time in the concrete phase to students who need it, but keep the tasks crisp. Build, say, and check. For example, in addition within twenty, have the child build two piles with linking cubes, say the story in a full sentence, and check by matching to a bar sketch.

Do not flood them with steps. Keep a steady rhythm they can master. As they succeed, move to representational drawings that mirror the builds they know well. When they draw what they built, they feel smart because the drawing is just a picture of a success they already had.

Use quick wins to build momentum. Choose number ranges where success comes often, then widen slowly. If a child can add within ten with ease after building, shift to within twenty using the same model.

Keep the language identical so it feels like more of the same, not a new mountain. Praise the model and the explanation more than the speed. Confidence grows when students believe they know what they are doing, not when they feel rushed to go faster.

Target vocabulary gently and often. Many struggling students know how to move pieces but cannot label what they are doing. Spend one minute per lesson on exact words tied to the model. Ask, what is the whole here, what is the unit, where is the rate.

Let them point and speak. This habit tightens understanding and helps them track steps without getting lost.

Add spaced review to lock gains. Two days after a new skill, bring back one short item that uses the same model. A week later, bring one more. Each revisit tells the student, you can still do this, and here is the same picture to help.

The feeling of return is powerful, especially for learners who fear forgetting.

Parents can support by keeping a small tool kit at home. A handful of counters, scrap paper for bars and arrays, and a mini whiteboard are enough. When homework stalls, say, show me the model first.

Then move to numbers. Over weeks, you will see fewer stalls and more steady progress. The gap narrows because the path is visible and kind, and the student walks it with growing control.

13. 48% improvement in word-problem accuracy when concrete models precede symbols

Word problems ask children to turn stories into math. Many errors happen before any numbers are written, because the story is fuzzy in the child’s mind. When we start with concrete models, accuracy rises sharply.

The child first acts out the story with real objects. This turns the hidden structure into something they can see and touch. Then they draw what they built, and only then do they write equations. By the time symbols appear, the child already knows what each number stands for and where the answer will live.

Begin with quick story builds. Read the problem once, slowly. Hand the child a small set of counters or cut paper bars. Ask them to show the story, not to solve yet. If the problem says that Mia has three bags with four apples each, the child should place three groups of four.

If the story says a tank is filled to three fifths and then more water is added, the child should shade three out of five parts on a strip and plan where extra shading would go.

When the build matches the story, pause and ask the child to state what each part means in a clear sentence. This ties language to action.

Move to a fast sketch that mirrors the objects. Keep drawings neat and small. A clean bar model, a ratio table, or a number line is enough. Invite the child to label units and unknowns. Circle what is asked.

Only after this step do you write equations. Now the symbols feel like names for parts the child already understands. If the child gets stuck later, direct them back to the drawing, not to guessing. The picture is the guide.

Add a daily two-minute routine called story to sketch. Give one short word problem. No numbers are large. The child must draw and label a model but not compute. This builds the habit of modeling first under gentle time.

At home, parents can ask for a one-sentence retell: tell me the story in math words. The more a child can retell a story with units and parts, the cleaner their later steps will be.

When this flow becomes normal, word problems stop feeling like tricks and start feeling like puzzles with clear pieces. Children read, build, draw, then compute. Accuracy climbs because sense-making comes first, and symbols follow the sense, not the other way around.

14. 1.9× increase in correct representation-to-equation mapping

A powerful turning point in math is when a child can look at a model and write the exact equation that matches it. This mapping skill is where many students stumble.

They might draw a fine picture but then write an equation that does not fit. When explicit mapping practice is added, correct matches nearly double. The idea is simple. Teach students to read a model like a sentence and translate line by line.

Start by choosing one model type per week. For example, spend a week on bar models for part–whole and difference stories. Each day, present three quick sketches and ask students to write the equation that fits each one.

Keep numbers small. Under the bars, write labels like part, part, whole, or start, change, result. The student points to each section and says what it becomes in symbols. If two small bars combine into one long bar, the sentence becomes a plus equation.

If a long bar is split by a bracket showing a missing piece, the sentence becomes a minus equation. The spoken rule stays steady: the model decides the operation.

Reverse the routine the next week. Give equations and ask for matching sketches. Children draw the bars or the number line that would make that equation feel obvious. This back-and-forth builds a tight link both ways.

If the mapping is wrong, do not correct the equation first. Fix the meaning. Ask, where is the unknown. Which part of the picture shows that. When the meaning lines up, the equation usually fixes itself.

Create a small mapping checklist students whisper before they write. What are the units. What is known. What is unknown. What is the operation the model shows. This takes only a few seconds and stops wild guesses.

During practice, color-code labels lightly. Unknowns get a small star or a soft highlight. This keeps the focus on what the equation must solve for, not just on moving numbers around.

Parents can help by asking for a “read the picture” step during homework. The child should touch each part of the sketch and say what it stands for in the story. Once they can do that, the equation becomes a direct translation, not a guess.

With steady mapping practice, drawings and symbols stop living in separate worlds. They work together, and accuracy climbs as the two languages become one.

15. 43% higher persistence (time-on-task) during abstract tasks following hands-on cycles

Persistence is the quiet engine behind success. It is the will to stay with a hard task without giving up. After students rotate through hands-on cycles before abstract work, they stick with tough problems much longer.

This rise in time-on-task comes from confidence and clarity. When a child has already built and drawn the idea, the abstract version feels like familiar ground. The mind is less likely to panic. The student keeps going because the path is visible.

Design short learning cycles that end just before fatigue. Begin with a two-minute build, followed by a one-minute sketch, and then move into eight to ten minutes of abstract practice.

Keep the build tiny and focused on the one structure you want to live in the child’s head. Do not turn the build into a long craft. The goal is a quick wake-up for the model. The sketch then freezes that model on paper. Finally, the abstract items flow from that frozen plan.

Teach students a simple self-talk line they can use when they hit a snag. What picture fits this, and where am I in the picture. This line pulls them back to the model instead of into worry. Train a second line for the next step.

What is one small move I can try. Encourage writing that next move without judging the whole problem. One small correct move often unlocks the next one, and motion itself builds persistence.

Use tiny stamina timers. Set a two-minute keep-going timer during challenging sets. The rule is simple.

Until the timer ends, the student must either sketch, label, or compute. No staring at the page. When the timer rings, they can take a ten-second breath and reset for the next short burst. These micro-bursts keep the brain engaged without draining it. Over days, extend the bursts gently.

At home, parents can model calm during struggle. When a child says this is hard, reply we have a plan. Show me the model first. Then pick one move. Praise the act of staying with the plan more than the final score.

Children notice what adults value. If we value process and steady effort, they learn to value it too. After a few weeks, you will see longer focus, fewer mid-problem freezes, and a stronger habit of using models to stay on track.

16. 27% drop in math anxiety scores during the transition phase

Anxiety blocks thinking. When a child feels tense, working memory shrinks, and even simple steps feel heavy. During a careful move from manipulatives to mental models, anxiety falls by over a quarter.

This drop happens because the child is not thrown into symbols cold. They travel a path they know. First they build, then they draw, then they solve. Each stage gives proof that they can do it, so fear has less room to grow.

To make this drop real, use a steady routine that never surprises the learner. Begin each session with a one-minute success replay. Ask the child to name one model they used yesterday and one small win. Keep it short and true.

Success remembered becomes confidence today. During practice, normalize tiny pauses. Teach a quiet breath and a line of self-talk: I can see it, I can sketch it, then I can solve it. The breath slows the body, and the line reminds the mind of the plan.

Lower the stakes while keeping standards high. Offer frequent try-again chances without penalty in the early abstract phase. The rule is simple. If a step does not match the model, circle, reset, and write a clean line.

Mistakes are normal; ignoring the model is the only error. This framing reduces panic. The child learns that control returns the moment they return to the model.

Use prediction to cut fear. Before solving, ask, about how big should the answer be. Should it be more or less than the starting number. Should it be near ten, near one, or much larger. When the answer arrives, compare it with the prediction.

If the two match, the brain relaxes. If not, the child sees a guidepost for correction instead of a dead end.

Parents can help at home by keeping talk gentle and concrete. Replace be careful with show me the picture. Replace hurry up with take one breath and find your first move. Praise calm steps, not speed alone.

If your child feels the room is safe, the math will feel safer too. Over a few weeks, you will see smoother faces, fewer freezes, and steadier hands.

If you want expert-led support that keeps stress low and confidence high, book a free trial class at Debsie today and watch your child’s worry turn into daily wins.

17. 2.7× improvement in flexible strategy switching (counting → decomposition → algebraic)

Strong learners do not stick to one method. They switch strategies when the problem changes. After a full transition to mental models, students are almost three times more likely to shift smoothly from counting to decomposition to algebraic thinking as needed.

This flexibility grows because models make the structure visible. When you can see the parts and the whole, you can choose a smart move for this exact problem, not just the last one you solved.

Teach a three-step switch routine. First, name the current strategy. Second, test the fit by checking the model. Third, switch if the fit is poor. For example, a child might start 18 + 27 by counting on. After sketching two bars, they notice an easier move: make a ten by taking two from twenty-seven and adding it to eighteen.

They switch to decomposition and finish fast. In ratio problems, a student may begin with a table and then notice a constant multiplier, so they jump to an equation. The model acts like a signpost that says, faster path this way.

Give short tasks that require a mid-problem switch. Set up items where counting works at first but becomes clumsy by the third step. Ask the child to circle the moment the original strategy slows down and write the new strategy above the next line.

Over time, this makes switching feel normal, not like giving up. It shows the learner that smart thinkers adjust.

Build a shared bank of named moves. Decompose to make a ten, trade a ten into ones, double and half, scale up, scale down, find the unit rate, set up a balance. Use the same names every time. When students can name a move, they can call it when needed.

Ask them, which move fits this picture best. If they can answer, the switch will feel obvious.

At home, invite quick what else moments. After your child solves, ask, could there be a faster way next time. Let them replay the model and point to a different move, even if they already got the right answer. This keeps the mind flexible and alert. It trains the habit of searching for elegance, not just arrival.

For guided practice that builds a deep catalog of strategies and the wisdom to switch, explore Debsie’s live classes.

Your child will learn when to count, when to break apart, and when to write an equation—with confidence and ease.

18. 39% more accurate estimation before calculation after model internalization

Estimation is the quiet check that stops wild answers from slipping through. When students carry strong mental models, their estimates get much closer to the truth.

Accuracy rises because the model tells the mind what “makes sense” before any detailed work begins. If a child sees a bar for 48% of a tank and adds about half again, they expect a number near three quarters, not past full. That early sense keeps later steps on track.

Make estimation a first move, not an afterthought. Before any arithmetic, ask, what do you expect roughly. Make the estimate visible in a light pencil above the problem. Keep it simple. Round to friendly numbers, lean on halves and tens, and use the model to reason.

With multiplication, an array picture helps. If the array is about seven by three, say roughly twenty. With division, a number line of equal jumps helps. If twelve splits into groups of five, say a bit more than two groups.

Teach three quick estimation frames. Benchmark to ten, to one, or to one hundred depending on the unit. Compare to half or double using a bar model. And cluster by rounding both numbers toward easier pairs that keep the product or sum close.

Keep the language short. About ten, about half, about double. These tiny phrases stick in a child’s talk and guide the hand.

Always reconcile the final answer with the estimate. Write a short check line. My answer is near my estimate because the model shows… If the answer is far off, start the fix by revisiting the model, not by hunting for a lost digit.

Ask, did I choose a wrong operation for this picture. Did I misplace the unknown. Often, aligning meaning repairs the number fast.

Parents can fold estimation into daily life. At the store, ask, if each snack is about thirty, what will three cost. On a walk, ask, if we have ten minutes left and we walk about two minutes per block, how many blocks can we do. Keep it light. The goal is to make estimation feel like common sense.

If you want a simple, friendly way for your child to build strong estimation habits that prevent avoidable errors, join a Debsie session. We model, we estimate, we solve, and kids learn to trust their number sense from the very first step.

19. 46% increase in spaced-retrieval quiz scores using mental imagery cues

Spaced retrieval is simple. Learn today, test a little tomorrow, test again a few days later, then again next week. When you add short mental imagery cues to this pattern, quiz scores jump almost by half.

The cue is a tiny picture or phrase that unlocks the model in the mind. It might be a quick mental bar, a dot array, or a number line with one bright tick. The cue does not replace practice. It makes practice stick by giving the brain a fast path back to meaning.

Start with a cue bank. For each unit, choose one image and one three-word tag. For fractions, the image might be a bar split into equal parts and the tag could be parts make whole. For ratios, a double line with matching tick marks and the tag keep the scale.

For equations, a balance sketch and the tag same both sides. Teach the cue on day one with manipulatives, repeat it with a drawing, and then ask students to close their eyes and picture it. Have them whisper the tag as they see the image.

Build a spaced plan that takes only minutes. On day two, ask two quick retrieval questions using only the cue and the tag, no notes. On day five, repeat with one fresh problem. On day twelve, repeat again. Keep items small so the routine never feels heavy.

Always start by showing the cue and saying the tag. Then hide the cue and have students picture it. This short step is what powers the jump in scores. It brings the model back before the numbers appear.

Teach students to write a micro-cue at the top of the page during quizzes. A tiny bar outline, two lines with arrows, or a balance symbol is enough. Next to it, write the tag. This takes five seconds and often saves five minutes of confusion later.

If a child freezes, they look at the cue, say the tag, and the path returns.

Parents can help with a quick dinner drill. Say the tag and ask your child to picture the image. Then give one small problem. After the answer, ask, did your picture help. Keep it light. The goal is confidence. Over a few weeks, you will notice that old topics come back quickly and cleanly.

If you want done-for-you cue banks and a spaced plan that fits real life, join a Debsie class. We blend imagery with retrieval so learning stays strong long after the unit ends.

20. 31% fewer reversals and misreads of inequality and operation symbols post-CRA

Symbol slips are common. Children flip a greater-than sign, read a minus as a plus, or treat a division bar like a fraction they must multiply. After CRA, these errors drop by about a third. The reason is that the symbol is no longer naked.

It is tied to a picture and a story. The model tells the symbol what to mean, so the eyes and hands follow the meaning rather than guessing from shape alone.

Begin with anchored symbols. For inequalities, anchor the sign to a number line. Have students place two numbers and stand a tiny arrow above the larger one. Then draw the mouth of the sign opening toward the bigger side.

Say the line aloud: the open side faces more. Repeat with bars of different lengths. For operations, anchor each symbol to one model. Plus is join bars. Minus is compare bars or remove a part. Multiply is equal groups or an array.

Divide is fair share or measure jumps. Keep these anchors steady for weeks so the brain builds automatic links.

Use slow look, quick act. Before writing a symbol, students pause, point to the model, and say what is happening. If they are joining parts, they say join, then write plus. If they are comparing who is larger, they say compare, then write the inequality facing the longer bar.

This two-second pause trains the hand to obey the model. Over time the pause shrinks, but the habit stays.

Add a daily five-symbol clinic. Present five tiny tasks mixed across operations and inequalities. Each task shows a simple model without numbers. Students must choose and write the correct symbol only, nothing else.

The set lasts one minute. Fast, clean, done. These micro-sets polish accuracy without draining attention from deeper problems.

When slips happen, correct the anchor, not the hand. Say, show me the model again. Ask, are we joining, removing, grouping, sharing, comparing. Once the student states the action, the correct symbol almost writes itself.

Parents can echo this at home. If a sign is wrong, point to the drawing and ask, what is happening here. Let the child fix the sign after naming the action.

At Debsie, we make symbols feel friendly by tying them to lived models first. Children stop fearing signs and start reading them as simple, honest actions. The result is a calm page with far fewer reversals and far more sense.

21. 54% rise in metacognitive “explain-your-model” responses on exit tickets

Metacognition means thinking about your thinking. When students explain their model at the end of a lesson, they grow this skill. With regular prompts, these explanations increase by more than half.

This is not about fancy paragraphs. It is about one or two clear sentences that say what picture they used and why it fit. When a child can do this, they are ready to guide themselves tomorrow without heavy teacher help.

Make the exit step small and steady. At the end of practice, ask two lines only. What model did you use. Why did it fit. Accept short, plain answers. I used a bar because there were parts that made a whole.

I used a table because the ratios needed equal steps. I used a number line because I had to track jumps of three. The aim is clarity, not style.

Seed the room with stems. I saw…, so I chose…, which showed… Encourage students to fill in with units, not just numbers. I saw cups and liters, so I chose a double number line, which showed the scale between them.

Over time, they start to use these stems without the poster. The stems become their inner voice when they sit down for a test or homework.

Turn explanations into next-day power. Begin the next lesson with a two-minute share of yesterday’s strongest explanations.

Ask the class to point to the part of the model that proves the claim. This makes the talk real and keeps the focus on evidence, not opinion. Invite a rewrite when needed. A child learns that clear thinking can be tuned and improved, just like any skill.

Use explanation as a repair tool. When a solution goes wrong, do not rewrite the steps. Ask for a model explanation first. If the explanation is thin or mismatched, rebuild the model, then try again. This keeps fixes tied to meaning rather than patching numbers.

Parents can try a bedtime recap. Ask, what picture helped you today, and why did it help. Keep it under a minute. The goal is to end the day with a small win and a feeling of control. These tiny reflections add up. Children begin to enter new problems with a plan already forming.

If you would like ready-made exit tickets and metacognitive stems you can use tomorrow, Debsie’s curriculum includes them in every unit. They are short, friendly, and powerful.

22. 2.3× improvement in proportional reasoning items after ratio-table manipulatives

Proportional reasoning is the heartbeat of middle school math and a core skill for science and daily life. When students first build ratio tables with real objects and tiles, then sketch the same table, and finally write numbers alone, their correct answers on proportion questions rise more than twofold.

The reason is clear. A ratio table shows the structure at a glance. It lines up pairs, keeps units honest, and makes scale jumps easy to see. Hands-on tiles make this even stronger because the child can slide groups, double them, or split them while talking through the meaning.

Start the journey with a simple story. If three cups of juice need two scoops of mix, show three cup tiles on one side and two scoop tiles on the other. Ask the child to double both sides by placing new tiles under the first row. Name it as you build.

Three cups go with two scoops. Six cups go with four scoops. Nine cups go with six scoops. This chant links each row. Then draw a neat table with two columns labeled cups and scoops. Copy the rows. Only after the table is clear do you write the numbers alone.

The order matters because the hands slow the mind just enough to notice the pattern.

Teach two faithful moves on the table. Scale up or down by the same factor and combine rows to form new rows. When children can say, I multiplied both columns by three, or, I added the first and second row to make the third, they stop guessing and start reasoning.

Invite them to point to the row that answers the question. This keeps the search focused and prevents random arithmetic.

Add quick comparison challenges. Place two tables side by side with different pairs. Ask which recipe is stronger, which speed is faster, or which deal is better. Encourage the child to find a common row by scaling or to compute the unit rate once and compare.

The table keeps the thinking tidy, and the answer feels fair because the units match.

Parents can bring this to life at home with cooking, shopping, or travel times. If one recipe uses two cups of flour for three pancakes, ask how many cups for nine. If a car goes sixty kilometers in one hour, ask how far in two and a half hours.

Encourage a tiny drawn table on a sticky note. Over weeks, your child will see ratios as friendly pairs that follow rules, not as traps.

For expert-led practice where ratio sense becomes second nature, try a free Debsie class. We build, we table, and we solve until proportional reasoning feels simple, strong, and sure.

23. 35% faster recall of key schemas (part–whole, comparison, change) during tests

Behind many problems sit a few core schemas. Part–whole covers totals and missing pieces. Comparison covers more than or less than. Change covers start, change, and result.

When students practice naming and modeling these schemas from concrete to mental, their recall during tests speeds up by over a third. Faster recall means quicker starts, fewer false trails, and more energy for careful calculation.

Begin with a schema warm-up that lasts two minutes. Say a short story without numbers. For part–whole, say there are some red marbles and some blue marbles that make a jar. For comparison, say one stack is taller than another.

For change, say a tank had some water, then more was added. Ask the child to choose a model shape. A bar with two parts for part–whole. Two bars side by side with a small bracket for comparison. A bar with a starting part and an added part for change.

Only after the shape is chosen do you add numbers. This keeps the schema choice pure and quick.

Train a four-word schema check before solving any problem. What story is this. The child answers with part–whole, comparison, or change. Then they draw the matching shape in five seconds. If they hesitate, return to the no-number warm-ups for a day.

The goal is automatic recognition. This is like seeing a road sign on a highway. You do not stop to read every letter. You recognize the sign and know what to do.

During practice, mix small problems across all three schemas so the child cannot guess the pattern. Keep numbers friendly at first. Ask them to say, I chose comparison because the story used more than, or I chose change because something was added.

This talk welds words to shape and shape to choice. On test day, the choice will pop up fast because it has been practiced under gentle pressure.

Parents can help by turning daily moments into schema games. If you pour juice from one cup to another, ask is this part–whole, comparison, or change. If prices go up in a store, ask which schema fits.

Short, playful rounds build quick recognition that transfers to paper. With this speed, your child starts strong on each problem, which lowers stress and raises scores.

If you want your child to build instant schema sense with clear visuals and friendly practice, Debsie’s sessions include daily schema warm-ups that make quick starts feel natural.

24. 44% improvement on near-transfer items and 26% on far-transfer items after fading

Near transfer means solving a new problem that looks a lot like what you practiced. Far transfer means solving something that looks different on the surface but shares the same deep idea.

After careful fading of manipulatives, both rise—near by almost half, far by about a quarter. This shows that fading does more than remove tools. It trains the mind to carry the model into fresh situations, even when the numbers, words, or layouts shift.

Plan fading in three gentle phases. In phase one, build and solve with tools every time, but add a short sketch after each build. In phase two, start with a sketch and keep tools only for checking.

In phase three, start abstract, then sketch only if stuck, and check with tools at the end. Keep the same problem types across phases so the child sees that only the support is changing, not the idea. This steady rhythm grows courage without creating shock.

To raise near transfer, vary small details while keeping the schema fixed. Change the numbers, swap names, or move the unknown from the end to the middle. Ask the child to state what stayed the same and what changed.

This trains attention on structure. To push far transfer, change the surface more boldly. Use a table instead of a paragraph, a diagram instead of a story, or a real-world task instead of a worksheet item. Always ask for the model choice first. When the model matches, the rest will follow.

Teach a two-part transfer script the child can whisper. What old idea hides here, and which model shows it. Encourage them to write that idea above the problem in three words.

If a rate problem hides inside a travel story, they might write speed times time. If a fraction comparison hides in a recipe, they might write same whole first. This tiny label keeps the brain locked on meaning while the hands work the steps.

Parents can support by asking bridge questions. When homework introduces a new-looking problem, ask what does this remind you of. Let your child point to a past model. If they struggle, show two options and let them choose.

The act of linking old to new is the heart of transfer, and it becomes easier each time you name it.

For families who want transfer to show up on tests and in real life, Debsie’s curriculum weaves fading, structure talk, and mixed-format practice into every unit. Children learn to spot the old idea inside the new wrapper and solve with confidence.

25. 63% of students can generate two or more mental models for the same problem

When a child can show one problem in two clear ways, understanding deepens and error risk drops. This stat tells us that almost two thirds of students reach true flexibility after a careful shift from manipulatives to mental models.

They might represent the same ratio with a double number line and a table, or show a fraction comparison with a bar model and a number line. This is not redundancy. It is insurance. If one model stalls, the other unlocks the path.

Build this habit with a routine called two windows. Present a problem and ask for the best-fit model first. Once it is drawn and labeled, invite a second, different model that tells the same story. Keep both small and neat.

Have the child write a one-line link between the two. For instance, the left window shows a bar split into fifths, while the right window shows the same fifths on a number line from zero to one. That single sentence ties the ideas together in the child’s mind.

Rotate pairings across the week. Bar to number line. Table to equation. Array to area model. Balance to inverse operation. As children practice, they begin to predict which second model will be most helpful.

On test day, they will have options. If a bar sketch feels messy, they can jump to a quick table. If an equation looks strange, they can check with a number line. Choice lowers stress and raises accuracy.

Use short compare prompts to strengthen transfer. After drawing two models, ask which one made the key step clearer and why. Keep answers brief and rooted in units. I saw equal jumps on the number line, so the scale factor was obvious.

Or the table made the unit rate visible, so the last step was easy. These comments sharpen metacognition without heavy writing.

Parents can support at home with quick double-takes. After your child solves, say show me a second way in thirty seconds. Do not demand perfection. Reward clarity and correct labeling.

Over time, your child will reach for a second model when the first one blurs, and the problem will unstick. If you would like structured lessons that bake in the two windows routine, Debsie’s live classes make flexibility a daily skill, not a rare moment.

26. 28% increase in homework completion when tasks require drawn models, not blocks

Homework completion rises when tasks feel doable and meaningful. Requiring drawn models instead of physical blocks at home raises completion by more than a quarter. The reason is practical and cognitive.

Families may not have manipulatives handy, and even if they do, setup takes time. A pencil sketch is fast. More important, a drawing is the bridge between hands and head. It keeps the structure clear while making the work portable.

Design homework so the first step is a tiny sketch box on each item. Ask students to draw the model in five lines or fewer, label units, and circle the unknown. Keep numbers friendly so the focus stays on modeling, not heavy computation.

Include one line for prediction based on the model, then the final calculation. This flow makes the page feel guided, not blank and scary.

Teach a home routine called picture first, numbers next. In class, practice this rhythm until it is automatic. Send home a one-page reference with three sample sketches for common stories: part–whole bar, double number line, and array.

Encourage families to post it near the homework space. The aim is quick starts. When children start fast, they finish more often.

Add tiny feedback loops that fit real life. Ask students to put a star next to the sketch that helped most and a dot next to a sketch that felt messy. Collect this info weekly and reteach the messy model with easier numbers and clearer labels.

When students see their feedback shape next week’s lesson, buy-in rises and completion follows.

Parents can help by asking for the smallest useful step. Instead of how much homework is left, ask show me your first sketch. Praise tidy labels and honest attempts, not perfect art. If frustration appears, reset with a single model and a small number set, then return to the original item.

That short detour often breaks the stall.

For families who want stress-free homework habits and clear modeling guides, Debsie includes parent-friendly sheets with every unit. They are short, simple, and help kids start fast and finish strong.

27. 4.6-point average gain on standardized conceptual subscales (out of 20)

Conceptual subscales measure whether students truly understand ideas, not just procedures. A 4.6-point average gain on a twenty-point scale is a big move. It means more correct answers on items that ask why an operation fits, what a fraction means, or how a variable represents an unknown.

These gains come from anchoring every skill in a model first, then moving to symbols with the model still in view.

Plan for concept-first lessons. Open with a short story or simple build that exposes the structure, then compress it into a sketch, and finally write the formal notation.

Keep the three steps tight so students feel the flow: from touch, to picture, to symbol. Require a one-sentence why after solving. I used a bar because the problem was part–whole. The why cements the concept and makes test explanations easier.

Map standards to models. For each tested idea, choose one reliable representation. Equivalent fractions live on number lines and bar partitions. Proportions live in ratio tables and double lines. Linear relationships live in t-charts, balances, and graphs.

Post these pairings and practice retrieval until students can name the model without looking. On test day, they will carry those maps in their heads.

Use quick contrast to highlight meaning. Present two near-miss items side by side and ask which model fits each and why.

For example, compare a join story and a compare story, both using similar numbers. The contrast sharpens schema recognition and prevents picking the right operation for the wrong reason. Keep computation small so the mind can focus on concept.

During review, rotate formats. A concept that holds across a table, a graph, a sketch, and a short story is sturdy. Require students to explain the link in one or two sentences. This simple crosswalk boosts transfer to unfamiliar test layouts.

Parents can support by asking why with kindness. After your child answers, say tell me how you knew to choose that model. Keep it brief. Praise clear reasons. Over time, your child will learn to lead with meaning and back it with method, the exact blend that concept tests reward.

If you want targeted prep that makes conceptual items feel comfortable, Debsie’s sessions integrate model mapping, contrast tasks, and tight explanations. Students learn to show understanding first and compute with confidence second.

28. 37% reduction in cognitive load ratings during abstract practice after rehearsal

Cognitive load is the weight on a learner’s working memory. When that weight is too high, the mind drops steps, misreads signs, and forgets what the question asked. After short, targeted rehearsal before abstract work, students report over a third less mental strain.

Lower load means more room for planning, checking, and finishing.

Rehearsal is not long review. It is a brief priming routine that reloads the needed model and language right before the hard part. Keep it under three minutes. First, cue the model with a tiny sketch. If today’s work is on ratios, draw a two-line scale and label units.

Second, say the two or three key words aloud—unit rate, scale factor, same units. Third, write one example line that sets structure but stops before arithmetic. Now start the practice set while that structure is fresh. The warm start clears clutter from working memory because the plan is already in place.

Teach learners to chunk steps into small, named actions. For example, in division with remainders, chunk as set up, subtract, bring down, repeat. In solving proportions, chunk as pick table, fill knowns, scale both, check units.

Name the chunk out loud before writing. When steps have names, the brain holds them more easily. If stuck, the student knows which chunk to restart, rather than redoing everything.

Trim the page to reduce noise. Use consistent spacing, clear labels, and modest numbers at first.

Work left to right with steady margins for small notes. Encourage a five-second “margin whisper”: the student writes a tiny plan word in the margin—table, bar, balance—before any numbers. This single word keeps attention on the model and stops the mind from wandering.

Add micro-recovery moves for moments when load spikes. Teach a breath, a glance at the cue sketch, and one question: where is the unknown in my model. Answering that question snaps focus back to the heart of the problem.

Parents can support by lowering home distractions during homework. A clear table, a sharp pencil, and a quiet two-minute priming chat do more for thinking than long lectures.

If you want your child to feel lighter and think clearer during tough problems, Debsie’s classes build these priming habits into every session. Students start strong, stay organized, and finish with energy left over.

29. 1.7× increase in success on non-routine problems requiring schema adaptation

Non-routine problems do not follow a script. They bend familiar ideas or mix two structures at once. After students learn to adapt their schema on the fly, success rises by about seventy percent. The key is learning to spot what stays the same when the surface changes, and to reshape the model rather than abandon it.

Begin with a simple routine called same–change–choose. First, ask what is the same as problems you know. Name the deep idea, like part–whole or ratio growth. Second, ask what is different. Maybe the units switch mid-story, or the graph replaces a table, or the unknown moves to the middle.

Third, choose how to adapt the model. Perhaps you draw two linked bars instead of one, add a second scale to a number line, or split a table into before and after blocks. Writing two short lines—same and change—takes fifteen seconds and points the mind to structure, not decoration.

Practice model morphing with tiny drills. Take a standard bar model for a discount problem, then morph it for a tax-plus-discount problem by stacking two change bars in sequence. Take a ratio table for a recipe, then morph it for a shrinking recipe by dividing both columns.

Take a balance sketch for an equation, then morph it for two unknowns by adding a second line. Each morph shows that the base schema still works after a small edit. Confidence grows because students see that new is often just a twist on known.

Use try-storming instead of blank staring. Give students permission to draft a quick first sketch, test one move, and revise.

Keep the first sketches tiny. A wrong sketch is not failure; it is data. Teach them to write a three-word reason when they change course, such as units mismatched here. This builds a trail of sense-making and prevents random switching.

Add time-boxed sprints. Set three minutes for the first model attempt, one minute for a check against units, and two minutes to revise. The clock keeps motion without panic. End with a one-line explanation of the final model choice.

Over weeks, students learn to bend their schemas with purpose.

Parents can help by asking a single adaptive question at home: if your first picture feels off, how would you change it to match the story. A small nudge toward model editing keeps momentum alive.

For guided practice with rich, non-routine tasks, Debsie’s live sessions include weekly challenge sets that make adaptation a normal, joyful skill.

30. 50% higher long-term retention (8–12 weeks) when manipulatives are faded in three phases

Lasting learning is the goal. When manipulatives are faded through three clear phases, memory at two to three months improves by half. The phases are simple and kind to the brain. Phase one is build-and-draw.

Students use tools and then freeze the idea with a quick sketch every time. Phase two is draw-and-check. They start with the sketch and use tools only to confirm tricky steps. Phase three is think-and-verify.

They begin abstractly, sketch only if stuck, and check with tools at the end. The idea is to keep the model alive while the hands step back.

Lay out a calendar so everyone knows the rhythm. Weeks one to two, heavy build with drawings. Weeks three to four, drawings first and tools as backup. Weeks five to six, abstract starts with optional sketches. Keep reviews small but steady.

Insert two-minute recall tasks from past weeks every few days. Each revisit acts like a memory glue that stops forgetting before it grows.

Use anchor artifacts to support recall. A single page with the core model, labels, and two example lines can live in folders or on the wall. Encourage students to redraw the anchor from memory once a week.

Redrawing is stronger than rereading because it forces reconstruction, which strengthens the memory trace. If a redraw is shaky, return briefly to phase two for that idea, then resume abstract work.

Mix formats during the retention window. Solve one item as a story, one as a diagram, and one as a small table. Same idea, different looks. This variety tells the brain the idea matters across contexts.

End each mini-set by predicting where the answer sits in the model. The short prediction step acts as a retrieval cue weeks later.

Parents can lock in gains with tiny spirals. Every Sunday, ask for a sixty-second teach-back of last month’s model.

The child draws the key picture and explains one example in plain words. Keep it friendly. These teach-backs turn review into a family habit and make school tests feel like simple check-ins, not surprises.

If you want a done-for-you fading plan with calendars, anchor pages, and weekly spirals, Debsie’s program includes all three. Children move from blocks to brain with care, and the learning sticks long after the unit ends.

Conclusion

The journey from manipulatives to mental models is not a leap. It is a careful walk across a clear bridge. You start with touch so ideas feel real. You draw so ideas become organized. You think in symbols so ideas become portable and fast.

Along this path, children grow in speed, accuracy, confidence, and calm. They learn to plan before they act, to choose the right tool for the job, and to explain why a model fits.

They build life skills too: patience, focus, and smart problem-solving under pressure. The numbers you just read are not just statistics. They are signals that this approach works for real children in real classrooms and homes.

Other Research Reports By Debsie: